Some time ago, I found myself fascinated by alternative numeral systems, thanks in part to a video from a conlanger’s community. For those unfamiliar, conlangers are people who engage in constructing new languages — a pursuit fascinating in its own right. However, we won’t delve into this rabbit hole and stick to numeral systems as stated.
Numeral systems are a tool of notation in mathematics, and the significance of notation cannot be overstated. It offers fresh perspectives and sometimes can render difficult problems trivial just by power of its expressiveness. It’s noteworthy that the dawn of modern mathematics is often linked not to a novel discovery, but to a revolution in notation, as seen in al-Khwarizmi’s seminal work on algebra.
Let’s establish a way to denote numeral systems. Indeed, we’re introducing notation for notations, why do you ask?
Numeral systems are represented as follows:
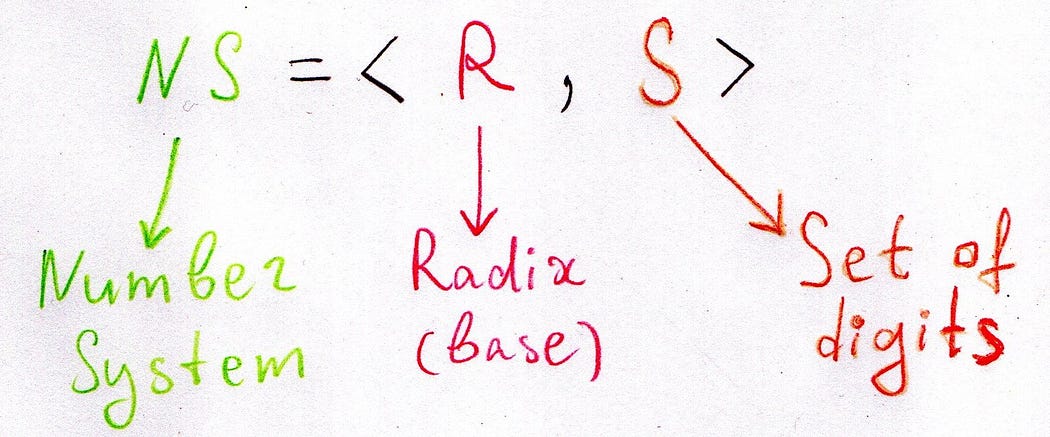
Our familiar base-10 system, for instance, is denoted by:
DEC = < 10, {0,1,2,3,4,5,6,7,8,9} >
But what exactly are digits? Consider them as the encoding method for numbers within a system. Thus, when we mention the number 123, we're referring to a concept that transcends notation but can be expressed differently across numeral systems:
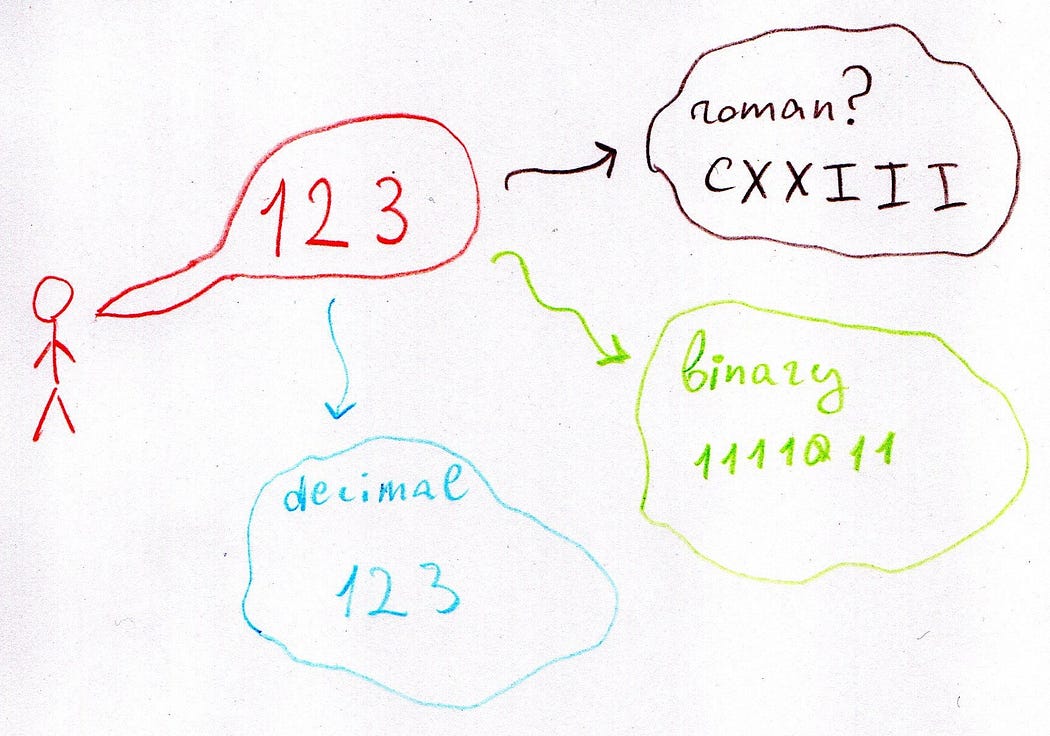
Digits, therefore, are the foundational elements of a numeral system, represented by distinct symbols without further encoding.
Balanced Ternary
Our journey into alternative numeral systems starts with the balanced ternary system denoted by

What catches the eye here is the inclusion of -1, which we’ll signify as ‘T’.
In this system, the initial numbers are represented as follows:
0 = 0
1 = 1
2 = 1T
3 = 10
4 = 11
5 = 1TT
Notice how `10` equates to 3, as expected in a base 3 system. However, there’s no single digit for 2; instead, we use ‘1T’ because 2 equals 3 minus 1 (2 = 10 + T in balanced ternary).
This leads to an intriguing observation about digit distribution. If we take any conventional numeral systems, usually denoted like this:
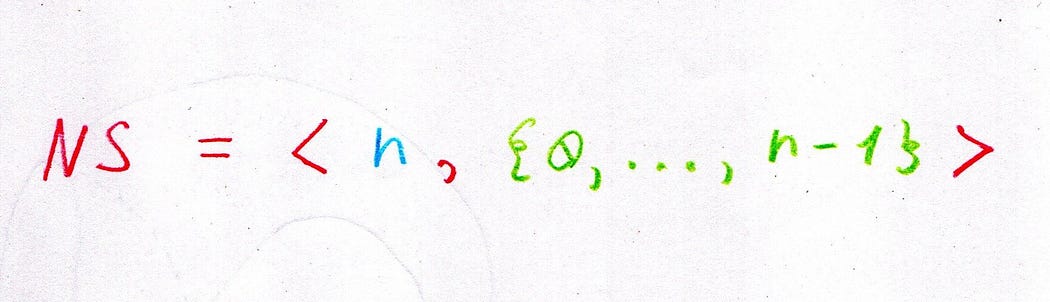
The number of digits in number’s representation notches up only after surpassing a power of the base. Yet, in balanced ternary, we’re already at two digits with ‘1T’ before hitting the first power of 3. This phenomenon reoccurs at each power of the base.
Even ‘0’ plays into this balance, serving as a pseudo-power of the base. It anchors the 1-digit numbers around itself, including negative values:
0 = 0
-1 = T
-2 = T1
-3 = T0
-4 = T1
-5 = T11
You could depict this digit distribution like this. Does this look a bit like scales?
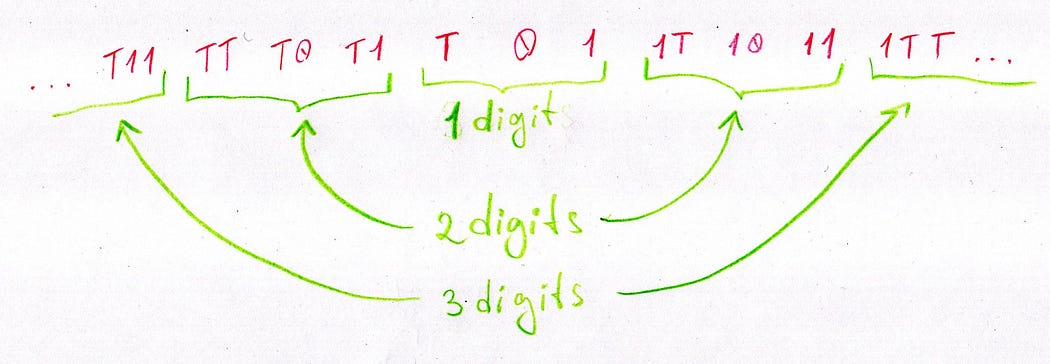
As you can see, we do not require a sign to represent negative numbers in this system. What other systems can we devise with the same intriguing feature?
You might wonder if we could get any “balanced -ary” numeral system? For example, we could choose 5 as our base, using digits {-2, -1, 0, 1, 2}, resulting in “balanced quinary”. What these bases share in common is their oddness, allowing us to “shift-and-balance” the digit set around zero. This balancing act is key to eliminating the need for a sign. But what about even bases? If is impossible to balance digits in even bases, but still there is a way.
Negative binary
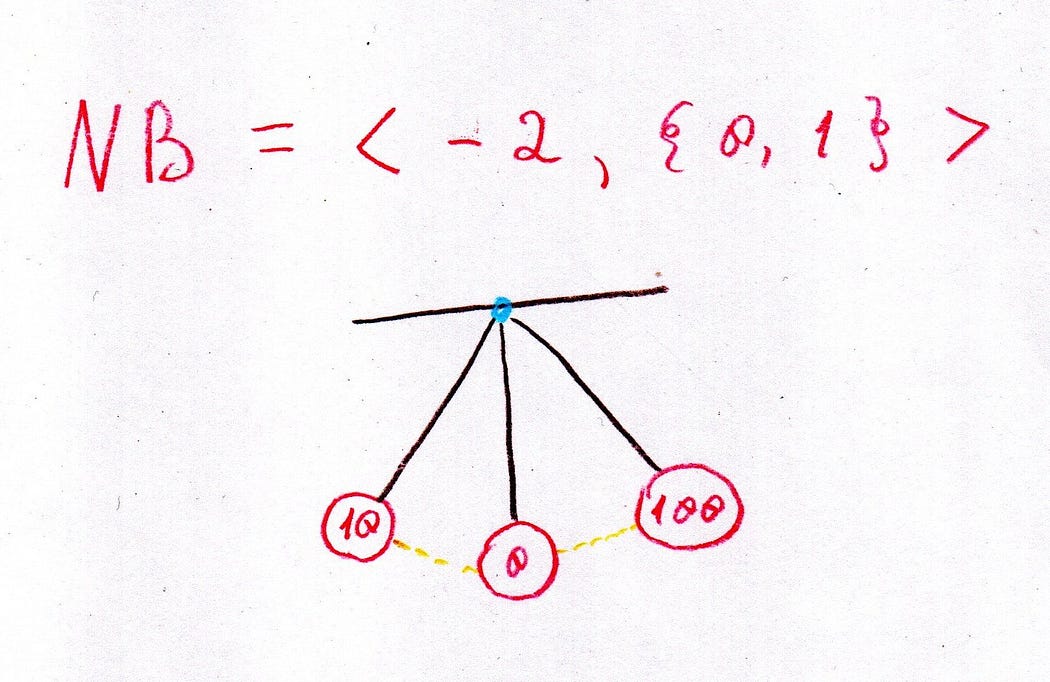
In negative binary (or negabinary) we are use a negative number as a base. This does not quite match up with our expectations:
2 = 10
1 = 11
0 = 0
1 = 1
2 = ???
Now what do we need to represent 2 in this system? Negative numbers have this convenient property that if you exponentiate them you will get different signs at each step:
4 = 100
5 = 101
And now we can go back to 2. 2 is just (-2)²+(-2). So that gives us a nice representation:
2 = 110
3 = 111
The long addition algorithm is particularly interesting in this system. To understand how it works we need to turn upside down all of our familiar notions on how two bits are added up, and this will suffice.
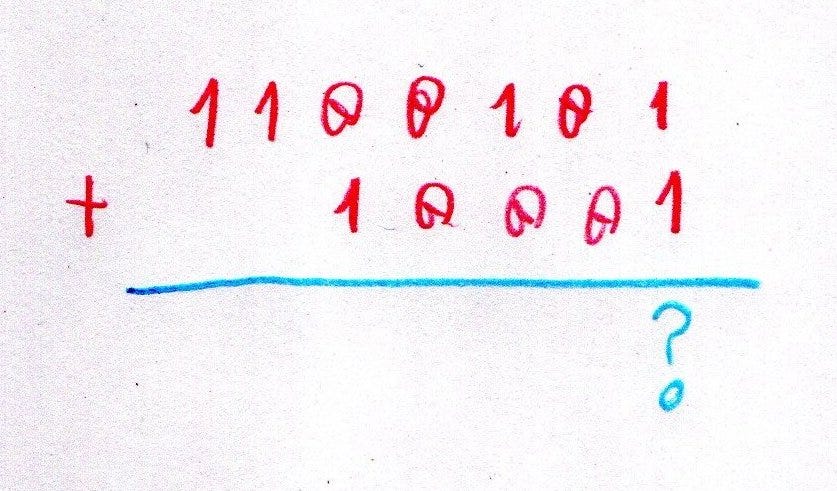
Let’s add digits from the first column. They’re both 1, so usually what we get in binary numeral system is 0 with 1 carried to the next column. But here what we get is 1+1=110. Let’s introduce just for a brief moment a negative sign into our notation, just for the purposes of long arithmetic. Then 1+1=-10. What that means is that we can carry a minus one to the next digit!
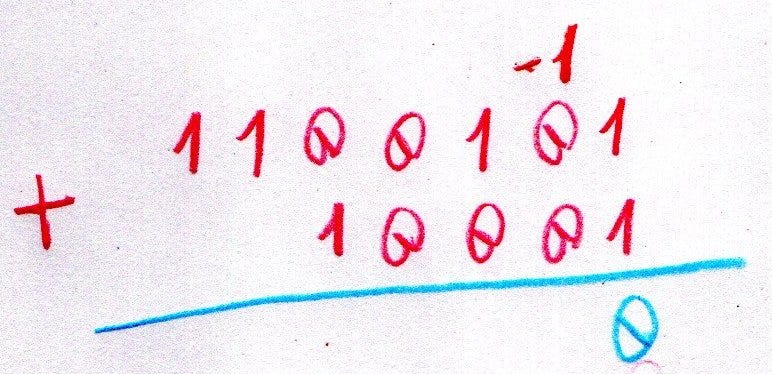
Now we are faced with 0–1. Usually we get 1 and carry a -1 to the next column. Here again with the upside down and we carry a 1 instead. Continuing this to the end:
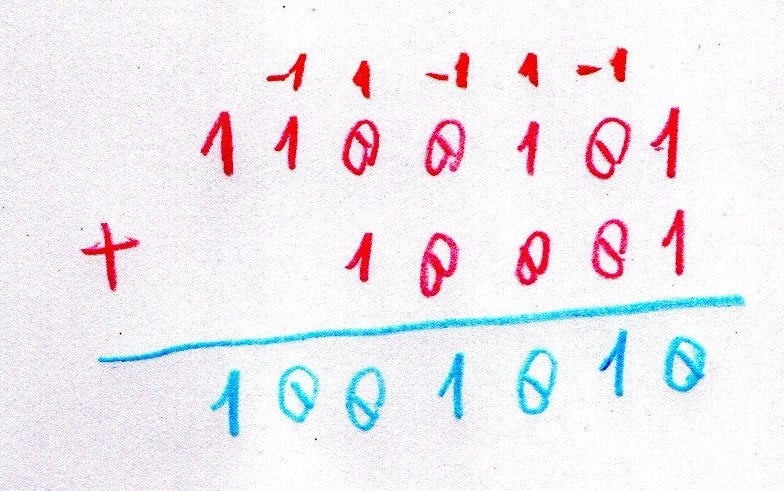
What about digit distribution? It oscillates between negative and positive numbers: 1 digit for positive integers, 2 for negative integers, 3 for positive integers, 4 for negative integers.
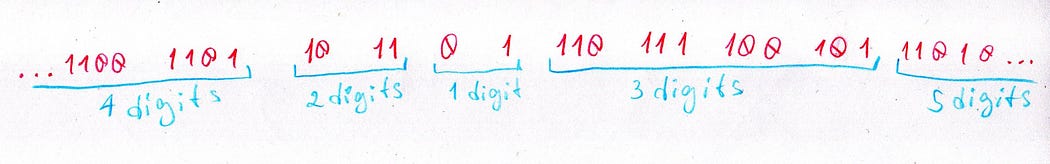
If we were to follow the naming style of “balanced ternary” for this concept, a fitting name for this numeral system could be “oscillating binary.”
Now, what if we try to merge these ideas? We could create a balanced negative ternary system with base -1 and digits {T,0,1}. What happens here — do we get oscillations, or does the balance take over? It’s actually not too tricky to work out, but observing how number’s representations weave in a such a wonderful way, I could not help myself but leave this as an exercise for the reader.
Non-integer numeral systems
This article is concerned with integer (non-natural) numeral systems, but there are also complex numeral systems. I'm not covering them here, but they create some extremely nice pictures. You can play around here.